भाग २

मोठमोठ्या संख्यांची बेरीज, गुणाकार, भागाकार तोंडी करत धडाधड अंगावर आकडे फेकणारे चाइल्ड प्रॉडिजी एकेकाळी सेलिब्रिटी म्हणून ओळखले जात होते. आपल्या येथे शकुंतलादेवी एक शीघ्र कॅल्क्युलेटर म्हणून गाजलेली होती. झचारियास डोज (Zacharias Dose) हा जर्मन चाइल्ड प्रॉडिजी 1844 च्या सुमारास प्रसिद्धीच्या झोतात होता. त्यालाही Π चे वेड लागले होते. त्याने 200 दशमान स्थानापर्यंत Π चे मूल्य निश्चित केले होते. या पूर्वीच्या गणितज्ञांप्रमाणे अनंत श्रेणीतील 100 - 200 पदांनंतरच Π च्या मूल्याच्या जवळपास जाणार्‍या समीकरणांचा वापर न करता त्याने यासाठी फार वेगळे समीकरण वापरले. त्याच्या समीकरणात प्रत्येक तिसर्‍या पदामध्ये 1/2, 1/5, व 1/8 पुन्हा पुन्हा येत होत्या. त्याने वापरलेले समीकरण

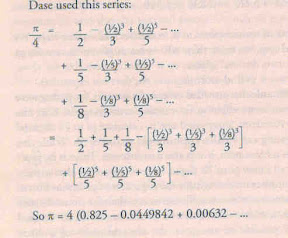
पहिल्या पदानंतर Π = 3.3

दुसर्‍या पदानंतर Π = 3.12

तिसर्‍या पदानंतर Π = 3.1452...

ब्रिटिश हौशी गणितज्ञ विलियम रुदरफोर्ड यांनी 440 दशमान स्थानापर्यंत अंदाज घेतला. अजून एक चाइल्ड प्रॉडिजी म्हणून नाव लौकिक मिळविलेल्या विलियम शांक्स यांनी 1853 मध्ये 707 दशमान स्थानापर्यंत मूल्य निश्चिती केली. 70 वर्षानंतर डी एफ फर्ग्युसन यांनी शांक्सच्या संख्येतील चूक शोधली. त्यामुळे 527 दशमान स्थानानंतरचे अंक बाद ठरले. दुसर्‍या जागतिक महायुद्धाच्या काळातही त्यांचा हा शोध चालू होता. 1945 पर्यंत 530, 1946 मध्ये 620, अंकांपर्यंत त्यांनी मजल मारली. फक्त कागद व पेन वापरून एवढ्या प्रमाणात आकडे तोपर्यंत कुणीही शोधले नव्हते.

Π च्या अंकांचा शोध घेणार्‍यात डी एफ फर्ग्युसन हा हाताने आकडेमोड करणारा शेवटचा व यंत्राचा वापर करणारा पहिला गणितज्ञ ठरला. नुकत्याच बाजारात आलेल्या डेस्क कॅल्क्युलेटरचा वापर करून वर्षभरात 200 दशमान स्थानापर्यंत अंकांची मांडणी त्याने केली. सप्टेंबर 1947 पर्यंत हा आकडा 808 पर्यंत पोचला. ENIAC संगणकाची रचना 1947 पर्यंत पूर्ण झाली होती. सप्टेंबर 1949मध्ये या मेन फ्रेम संगणकाचा वापर करून 2037 अंक वापरून 1000 दशमान स्थानापर्यंत Π चे अचूक मूल्य निर्धारित करण्यात आले.

Π चे आकडे फुगतच होते. व त्या आकड्यांकडे बारकाईने पाहिल्यानंतर त्यातून काही ठराविक आकृतीबंध (pattern) मिळतो का याचा शोध घेण्याचे प्रयत्न करण्यात आले. परंतु पदरी निराशाच आली. ठराविक अंकांची श्रेणी वा आकृतीबंध यात नाही हे 1761च्या सुमारासच तज्ञांना कळून चुकले होते. स्विस गणितज्ञ जोहान लँबार्ट यानी Π चे हे गुणविशेष हेरून त्याला √2, e प्रमाणे अपरिमेय संख्या म्हणून वर्गीकरण केले. Π चा दशमान विस्तार अनंतापर्यंत जाणारा व यादृच्छिक असणारा आहे यावर त्याकाळी शिक्कामोर्तब बसला होता. याच्याही पूर्वी फेर्डिनँड फॉन लिंडमन या जर्मन गणितज्ञानी Π ही संख्या अपरिमेय आहे असे विधान केले होते.

Π ही संख्या केवळ बौद्धिक व्यायामासाठी व मनोरंजनासाठी नसल्याचा प्रत्यय 18व्या व 19व्या शतकात येऊ लागला. 3.141592... या संख्येचा व्यावहारिक रित्या दरवाजे, खिडक्या यांच्या रचनेत वापरात येते हे लक्षात आले. धूर बाहेर ओकणार्‍या धूरचिमण्यांच्या रचनेत याचा वापर होऊ लागला. येवढेच नव्हे तर लंबकाच्या एका आंदोलनासाठी लागणारा वेळ व लोकसंख्येतील मृत्युच्या वितरणाचे प्रमाण निर्दिष्ट करण्यासाठी Π या संख्येला महत्व आहे हे लक्षात आले. एखादे नाणे 2n वेळा उडविल्यास व n ही संख्या फार मोठी असल्यास छाप:काटा याचे प्रमाण 50:50x1/√(nΠ) होईल, हेही लक्षात आले. फ्रान्स येथील बुफॉनचा काउंट असलेला जॉर्ज लुइ लीक्लर्क (Georges Louis Leclerc) याने Π संबंधात भरपूर विचार केला होता. जुगाराच्या अड्ड्यावरील निरीक्षणात Π चा वापर होऊ शकतो हे त्याचे विधान बुचकळ्यात टाकणारे होते. या काउंटनंतरचा पियरे सायमन लाप्लास (Pierre Simon Laplace) यांनीसुद्धा टायलिंग केलेल्या जमिनीवर सुयांचा मोठा गठ्ठा फेकल्यानंतर त्यातील काही सुया दोन टाइल्समध्ये जाण्याच्या प्रमाणावरून Π चे मूल्य निश्चित केले होते.

Π ही संख्या केवळ गणित विश्वातच नव्हे तर सांस्कृतिक विश्वातसुद्धा अमाप प्रसिद्धी मिळवत होती. Π मधील अंक वा अंकांची श्रेणी पुन्हा पुन्हा येत नसल्यामुळे स्मरणशक्तीच्या चाचणीसाठी याचा वारेमाप उपयोग होऊ लागला. 1838 साली एका 12 वर्षाच्या डच मुलाने Π मधील 155 अंक तोंडी म्हणून दाखविले होते. आकिरा हारागुची (Akira Haraguchi) या 60 वर्षाच्या जपानी अभियंत्याने 2006 साली 100000 अंक तोंडपाठ म्हणून दाखवत जागतिक दाखला प्रस्थापित केला. हे आकडे तोंडी म्हणण्यासाठी त्याला 16 तास 28 मिनिटे लागली. दर दोन तासानी फक्त 5 मिनिटं भाताचा मूद खाण्यासाठी विश्रांती घेत होता. त्याच्या दृष्टीने Π भोवती दैविक वलय होते.

काही जण हे अंक लक्षात ठेवण्यासाठी 3 वा 5 अंकांचा संच करतात. 1950च्या दशकात स्विडिश नागरिक मॅट्स बर्गस्टन (Mats Bergsten) यानी 3 चेंडू झेलत 3 च्या संचात 9778 अंक सांगू शकला! अजून एका स्पर्धेत 5 अंकांचे 2000 संच होते. व त्यातील पहिल्या संचात 14159 हे अंक होते. वेगवेगळ्या 50 संचातील अंक सांगितल्यावर स्मरणशक्ती वापरून संचांची क्रमवारी लावण्याची स्पर्धेची अट होती. अचूक उत्तर देणाऱ्या जगातील चार जणांपैकी मॅट्स बर्गस्टनही होता. त्यासाठी त्याला फक्त 17 मिनिटं 39 सेकंद एवढा वेळ लागला. आकिरा हारागुची एक लाख अंक लक्षात ठेवण्यासाठी स्मृतीसाधक सूत्रांचा (mnemonic) वापर करत होता. प्रत्येक अंकासाठी अर्थपूर्ण शब्द ठरवून त्यांचा वाक्यात वापर करत व वाक्य लक्षात ठेवून तो अंक सांगत होता. उदाहरणार्थ

How I need a drink, alcoholic in nature, after the heavy lectures involving quantum mechanics.

3.14159285358979

Howमध्ये 3 अक्षरं, I मध्ये 1 अक्षर व need मधील 4 अक्षरं या प्रकारे पहिल्या वाक्यातून 3.14159285358979 हे अंक लक्षात राहतील.

(आणखी काही उदाहरणं

"Can I have a Pepsi? Carbonate it please. Right now!" 3.141592653".

|श्रीराम|हे रघुवर तू सीतारमणा दशरथकुलभूषणा रामा कौसल्यानंदना......3.1415926)

(या संबंधीचीआणखी उदाहरणं )