√2 ही संख्या अपरिमेय असली तरी त्याबद्दल Π सारखे कष्ट घ्यायला कुणी तयार नव्हते. Πच्या अंकांचे कवितेत रूपांतर करणारे कवीसुद्धा त्याकाळी होते.

मुळात Π ही संज्ञा सर्वप्रथम 1706मध्ये विलियम जोन्स यांनी आपल्या गणितविषयीच्या पुस्तकात परिघ सूचित करण्यासाठी केली होती. परंतु हे ग्रीक अक्षर त्यावेळी रूढ झाले नव्हते. पुढे 30 वर्षानंतर लिओनाह्र्ड ऑयलर (Leonahrd Euler) यींनी Π संज्ञेला मानाचे स्थान प्राप्त करून दिले. 886 पुस्तकं लिहिणारा ऑयलर बहुश्रुत होता. Π बद्दल जास्त विस्ताराने विचार करणाऱ्यापैकी तो एक होता. 18व्या व 19व्या शतकातील Π अंकशोधक ऑयलरने वापरलेल्या सूत्राचा वापर करत होते. भारतीय गणितज्ञ श्रीनिवास रामानुजन यांनीसुद्धा या शोधात रुची दाखवली होती. त्यांचे Π बद्दलचे सूत्र अशा प्रकारचे होते.

या सूत्राप्रमाणे n चे मूल्य वाढवत गेल्यास Π चे 6 दशमान स्थानापर्यंतचे अचूक मूल्य मिळू शकते. रामानुजनप्रमाणे ग्रेगरी व डेव्हिड चुड्नोव्ह्स्की (Gregory and David Chudnovsky) या बंधूद्वयानी 1980च्या सुमारास याच प्रकारचे सुधारित सूत्र वापरून 15 अंकापर्यंतचे अचूक मूल्य शोधले होते. त्यांनी वापरलेले सूत्र असे होते.

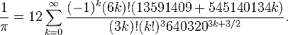
1950 -60च्या दशकात संगणक तंत्रज्ञानाचा वापर मोठ्या प्रमाणात होऊ लागला. Π मधील अंकांच्या शोधासाठी गणितज्ञ संगणकाची मदत घेऊ लागले. 1970च्या शेवटी शेवटी 10 लाख स्थानापर्यंत हे मूल्य पोचले. अत्यंत वेगवान संगणक व गणनविधीमुळे (algorithm) अंकांच्या शोधाला मोठी गती मिळाली. टोकियो विद्यापीठातील यासुमासा कानडा (Yasumasa Kanada) या तरुण संगणक तज्ञाने 1981 मध्ये NEC संगणकाचा वापर करून 137 संगणक-तासात 20 लाख स्थानापर्यंतचे अंक शोधून काढले. पुढील 3 वर्षात हा आकडा 160 लाखापर्यंत पोचला. कॅलिफोर्निया येथील विलियम गॉस्पर (William Gosper) या गणितज्ञाने ही संख्या 175 लाखापर्यंत नेली. नासाच्या डेव्हिड बेली (David Bailey) 290 लाख अंक शोधले. 1986 मध्ये यासुमासा कानडा यांनी पुन्हा एकदा 330 लाख अंक शोधून स्वत:चाच दाखला मोडला. पुढील 2 वर्षात S-820 संगणक वापरून त्यांनी 2010 लाख अंकांचा नवीन दाखला प्रस्थापित केला. यासाठी त्यांना फक्त 6 संगणक-तास एवढाच वेळ लागला.

इंटरनेटचा वापर वाढल्यानंतर चुड्नोव्ह्स्की बंधूनी स्वत:च्या संगणकाची जोडणी IBM सुपरसंगणकाशी केली. जेव्हा सुपरसंगणक रिकामा असेल तेव्हा चुड्नोव्ह्स्कीचे सूत्र वापरून सुपरसंगणक आकडेमोड करू लागले. उत्तरादाखल आलेले अंक चुड्नोव्ह्स्कीच्या पर्सनल संगणकात जमा होऊ लागले. 1991 पर्यंत या पद्धतीने तो 200 कोटी दशमान स्थानापर्यंत Π चे मूल्य निश्चित करू शकला. तोपर्यंत यासुमासा कानडा यानी 1.2 ट्रिलियनचा आकडा गाठला. 2008 साली हा आकडा 2.6 ट्रिलियन पोचला. 2009 साली चुड्नोव्ह्स्कीचे सूत्र वापरून फॅब्रैस बेलार्ड (Fabrice Belard) या फ्रेंच गणितज्ञाने डेस्क टॉप संगणक वापरून 2.7 ट्रिलियन अंक शोधले. त्यासाठी 131 संगणक-दिवस लागले होते. हे ट्रिलियन आकडे एका पानात अगदी बारीक फाँटमध्ये 5000 अंक लिहिले तरी ते सर्व अंक लिहिण्यासाठी 10 किलोमीटर उंचीचा कागदाचा गठ्ठा लागेल. परंतु हे सर्व का केले जाते? या प्रश्नाला उत्तर नाही. कदाचित जागतिक दाखले मोडण्यासाठीच असतात, असे या छंदिष्टांना वाटत असावे.

या व्यतिरिक्त अगदी टोकापर्यंत जाऊन Πचे अचूक मूल्याचा शोध घेण्यामागे अजून एक उद्दिष्ट साध्य होत असावे. यातून संगणकाच्या कार्यक्षमतेचा अंदाज, आकडेमोडीच्या प्रक्रियेचा वेग, संगणकाचा अचूकपणा इत्यादींची काटेकोर चाचणी घेणे शक्य होणार आहे. काही तज्ञांना Π मधील अंकांपेक्षा त्यासाठी वापरलेल्या गणनविधीत जास्त रुची असते. √2 वा eⁿ सारख्या अपरिमेय संख्येपेक्षा Π जास्त परिणामकारक आहे, असे तज्ञांचे मत आहे. संगणकातील मेमरी चिप्सच्या डिझाइनसाठी Π एक महत्वाचे टूल ठरत आहे.

कार्ल सॅगन या वैज्ञानिकाच्या काँटॅक्ट या गाजलेल्या वैज्ञानिक कादंबरीत एक ऍलियन पृथ्वीवरील महिलेला Π मधील यदृच्छता (randomness) संपून 0 व 1 या अंकाद्वारे काही सूचना मिळणार आहेत, असे सांगतो. व ही सूचना 10 ²⁰ स्थानानंतर येईल अशी कल्पना देतो. आज आपल्याला 2.7 ट्रिलियन (2.7x10¹²) अंक माहित आहेत. कदाचित नजीकच्या काळात आपण 10²⁰चा टप्पा पारही करू शकू. त्यानंतरच आपल्याला सॅगनच्या विधानातील सत्यासत्यतेचा अंदाज येऊ शकेल. त्यानी केलेले विधान केवळ कल्पनाभरारी नव्हती, हेही सिद्ध होऊ शकेल.

जरी Π ही संख्या अपरिमेय आहे हे गणितीय पद्धतीने सिद्ध झाले असले तरी हौशी गणितज्ञ व काही छांदिष्ट Π च्या अंकात आकृतीबंधाचा शोध घेतच आहेत. कदाचित 10²⁰ नंतर येणार्‍या 0 व 1 च्या श्रेणीनंतर हा आकृतीबंध ठळकपणे दिसू शकेल असे त्यांना वाटते. आजपर्यंत तरी गणितज्ञांना विशेष असे काहीही सापडले नाही. पहिला शून्य 32 व्या स्थानावर येतो. खरे पाहता यदृच्छाच्या गुणधर्माप्रमाणे शून्य यापेक्षा लवकर येण्याची अपेक्षा होती. 762व्या स्थानानंतर 9 हा अंक 6 वेळा लागोपाठ आला; 999999 . अशा प्रकारे एखादा अंक लागोपाठ 6 वेळा येण्याची शक्यता 0.1 टक्के असते. हा बिंदू फेनमन (Feynman) पॉइंट म्हणूनही ओळखला जातो. Π च्या अंकांची उजळणी करत करत या बिंदूपाशी आल्यानंतर 9, 9, 9, 9, .... असे म्हणत विधान पूर्ण करता येईल. या नंतर 9 हा अंक 6 वेळा 193034 स्थानानंतर आला आहे. 0123456789 हा संच 17387594880व्या स्थानानंतर दिसतो.

Π च्या अंकांची ही जादू न संपणारी आहे. या अंकांच्या श्रेणीत अनेकांना स्वत:ची जन्मतारीख, लग्नाचा वाढदिवस, फोन क्रमांक, गाडीचा क्रमांक इत्यादी दिसलेले आहेत. परंतु या संख्या कुठल्या स्थानानंतर दिसतात याचा शोध घेण्यातच खरी गंमत आहे व हा शोध कुठे ना कुठे तरी चालू आहे व तो अनंत काळापर्यंत चालू राहणार आहे.....

संदर्भ 1, 2, 3 , 4 Alex's Adventures in Numberland, Alex Bellos

या संबंधातील काही चित्रफीती:

http://www.youtube.com/embed/yJ-HwrOpIps
http://www.youtube.com/embed/mZ4CP0vTgEE
http://www.youtube.com/embed/2fCTnF75AL0